Searching Genomic Databases

Because of the nested for loops, the algorithm DynamicProgramming in the "Genomic Sequence Comparison" module has complexity O(mn), where m and n are the lengths of the sequences. Thus, for equal-length sequences, the complexity is quadratic, O(n2). If we are trying to find sequences that are similar either locally or globally to a given query sequence, dynamic programming for pairwise comparison of a query sequence with millions of entries in a database can take an excessive amount of time. For speed, various algorithms use heuristics that do not promise a best answer but that usually give an acceptable result.

In searching genomic databases, algorithms should produce scores that allow us to differentiate sequences that are related to a query sequence from those that are not. Similar sequences can help us determine the biochemistry, physiology, and function of a gene or the protein it produces.

We often score the similarity of proteins by determining the degree to which they are related through a common evolutionary ancestor. If the similarity score is high enough, we say the proteins are homologous. Through evolution, one amino acid might substitute for another, but such changes usually preserve the fundamental nature of the protein. Thus, if a database search finds a protein that is homologous to a query protein, information about a well-documented database protein can help us understand the newly discovered protein.

Similarity scoring should manifest the fact that some amino acid substitutions are more likely to occur than others. Also, because substitutions occur more frequently than deletions and insertions, gaps, or spaces in an alignment, should carry a lower weight.

The dynamic programming algorithm in the "Genomic Sequence Comparison" module gives the similarity score and optimal global, or overall, alignment for two sequences. Usually, database searches seek sequences that have high scores for local alignments with the query sequence. A local alignment of two sequences occurs between a pair of subsequences (or regions or segments) of the sequences.

Three of the main algorithms for database searching are Smith-Waterman, FASTA, and BLAST. The Smith-Waterman algorithm is the most rigorous of the three. This algorithm has a high degree of sensitivity in that it is able to recognize distantly related sequences. However, FASTA and BLAST are more selective in that these algorithms are better able to discard sequences that are not related to the query sequence. The slower Smith-Waterman algorithm does not use heuristics, while FASTA and BLAST do. We consider the Smith-Waterman and BLAST algorithms in this module
Smith-Waterman Algorithm

The rigorous Smith-Waterman algorithm is very similar to the dynamic programming algorithm. To obtain the best local alignment between a pair of sequences, the algorithm does not allow negative partial similarity scores to occur and to propagate. Thus, if a negative integer is the maximum of the three calculations, the algorithm places zero in the array entry. As the following formula shows, for k = 1 the only difference between the dynamic programming formula and the Smith-Waterman formula is the inclusion of zero in the list of items for which to find a maximum:


By zeroing out scores that fall into the negatives, we do not accumulate mismatches on the global level, and we allow scoring to start over on the local level. The sequences might be badly mismatched before certain regions in which they strongly agree.
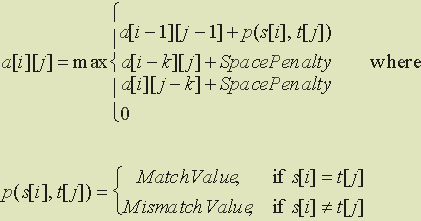
Example 1.    Using the Smith-Waterman algorithm with sequences s = CCTGAGTT and t = ACCTAGCGA, we determine the best local alignment and its similarity score. Suppose the space penalty is -7; the match value is +5; and the mismatch value is -4. Assume that initial gaps are worth 0, so that we initialize row 0 and column 0 with all zeros. Note that the letters C, T, G, and A could represent bases or amino acids. Moreover, the same algorithm applies to different letters.

Quick Review Question
Quick Review Question 1 Fill in the matrix values in row 4.

   
-
 
A
 
C
 
C
 
T
 
A
 
G
 
C
 
G
 
A
                                         
T
3
0
 
0
 
0
 
3
 
15
 
8
 
1
 
0
 
1
 
0
                                         
G
4
0
                                   



Click here for the completed matrix.

The maximum value in the table is 18. Following the line segments backward until arriving at a zero, we discover the best local alignment to be for the segment CCTGAG from s and CCT-AG from t, as follows:

Region in s:
C
C
T
G
A
G
Region in t:
C
C
T
-
A
G
 
Quick Review Question
Quick Review Question 2 Perform the Smith-Waterman algorithm on sequences s= ATGAC and t = ACGC. Find the best local alignment and its similarity score.

BLAST

The Smith-Waterman algorithm is guaranteed to find the best local alignment with respect to the given scoring for matches, mismatches, and spaces. BLAST does not necessarily find the best local alignment, but the algorithm does find reasonable answers quickly.

The BLAST algorithm uses a PAM (Point Accepted Mutations) scoring matrix. In the 1970s, a research team lead by Margaret Dayhoff carefully studied the evolution of sequences of amino acids. PAM or PAM 1 is the length of time for 1% of the amino acids to mutate. One estimate is that a PAM is about a million years. 1-PAM matrix is a matrix with column and row headings of the amino acids where entries represent the amount of evolution over one PAM period of time, or for one mutation per hundred amino acids. A 250-PAM matrix contains scoring information on the amount of evolution over 250 PAM periods of time. We can obtain this matrix by raising the 1-PAM matrix to the 250th power. Figure 1 contains 250-PAM scoring matrix.

Figure 1. The 250-PAM scoring matrix. B is used when one cannot distinguish between D and N because of amino acid analytical processing. Similarly, Z is used when it is ambiguous whether the amino acid is E or Q. X represents an unknown or nonstandard amino acid. Thus, the matrix has 23 rows and 23 columns. 
    A  R  N  D  C  Q  E  G  H  I  L  K  M  F  P  S  T  W  Y  V  B  Z  X
 A  2
 R -2  6
 N  0  0  2
 D  0 -1  2  4
 C -2 -4 -4 -5 12
 Q  0  1  1  2 -5  4
 E  0 -1  1  3 -5  2  4
 G  1 -3  0  1 -3 -1  0  5
 H -1  2  2  1 -3  3  1 -2  6
 I -1 -2 -2 -2 -2 -2 -2 -3 -2  5
 L -2 -3 -3 -4 -6 -2 -3 -4 -2  2  6
 K -1  3  1  0 -5  1  0 -2  0 -2 -3  5
 M -1  0 -2 -3 -5 -1 -2 -3 -2  2  4  0  6
 F -4 -4 -4 -6 -4 -5 -5 -5 -2  1  2 -5  0  9
 P  1  0 -1 -1 -3  0 -1 -1  0 -2 -3 -1 -2 -5  6
 S  1  0  1  0  0 -1  0  1 -1 -1 -3  0 -2 -3  1  2
 T  1 -1  0  0 -2 -1  0  0 -1  0 -2  0 -1 -3  0  1  3
 W -6  2 -4 -7 -8 -5 -7 -7 -3 -5 -2 -3 -4  0 -6 -2 -5 17
 Y -3 -4 -2 -4  0 -4 -4 -5  0 -1 -1 -4 -2  7 -5 -3 -3  0 10
 V  0 -2 -2 -2 -2 -2 -2 -1 -2  4  2 -2  2 -1 -1 -1  0 -6 -2  4
 B  0 -1  2  3 -4  1  2  0  1 -2 -3  1 -2 -5 -1  0  0 -5 -3 -2  2
 Z  0  0  1  3 -5  3  3 -1  2 -2 -3  0 -2 -5  0  0 -1 -6 -4 -2  2  3
 X  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
    A  R  N  D  C  Q  E  G  H  I  L  K  M  F  P  S  T  W  Y  V  B  Z  X

The BLAST algorithm usually employs the 120-PAM scoring mat, which represents the amount of amino acid evolution over 120 PAM epochs. The algorithm searches a database for sequences that have a "good", non-gapping local alignment with a segment of the query sequence. The program starts by breaking the query sequence into all possible sequential triplets, or 3-mers, or words of length 3. For example, if the query sequence is s = RHQMN, we have three 3-mers, as the following shows:
R
H
Q
M
N
R
H
Q
   
 
H
Q
M
 
   
Q
M
N

Using these words, the program compiles a list of all words that have a score greater than or equal to a certain threshold parameter. For example, using the 250-PAM matrix, QMN has a score of 4 + 6 + 2 = 12. The score for Q remaining Q is 4; the score for M not evolving over 250 PAMs is 6; and the N-to-N 250-PAM matrix score is 2. As another example, the scoring of QMN relative to pairs DLL, QSW, and BME is 3, -2, and 8, respectively, as the following computations indicate:
Q
 
M
 
N
   
D
 
L
 
L
   
2
+
4
+
(-3)
=
3
             
Q
 
M
 
N
   
Q
 
S
 
W
   
4
+
(-2)
+
(-4)
=
-2
             
Q
 
M
 
N
   
B
 
M
 
E
   
1
+
6
+
1
=
8

If the user picked a threshold value of 5, the program would select QMN and BME and others but not DLL and QSW as evolutionary matches. The BLAST program obtains the evolutionary score for all (23)(23)(23) = 12,167 possible amino acid triplets in relation to each of the 3-mers in the query sequence. (See note with Figure 1, which explains the need for 23 symbols.) Sometimes, a 3-mer that from the query sequence has a score that falls below the threshold, but the user has the option of including any query 3-mers.

Quick Review Question
Quick Review Question 3 For the sequence RHQM, how many scores would the program look up in a PAM matrix in determining 3-mers above a certain threshold?

Quick Review Question
Quick Review Question 4 Evaluate the 250-PAM matrix score for the word RHQ evolving to the amino acid sequence ACF.


The second step in BLAST is to scan the database for locations of high scoring words from the first step. For example, RHQ occurs at location 6 in the sequence NRSQHRHQLDLDMFPMST. One method of scanning a database utilizes a deterministic finite automaton (DFA) or finite state machine.

This "machine" is not a piece of hardware but is a mathematical model that we can use to recognize desirable sequences. This model has an input/output unit, and, consequently, has a way of communicating with the world using a set of symbols. In the present example, I, the set of input symbols, is the set of one-letter symbols for the amino acids. We do not use any output, but there is a set of states for our model. A state is like a snapshot of what is happening in the machine at a particular instant. For BLAST, a state indicates how far along we are in recognizing a high scoring word in a database sequence. The next state function or transition function returns the next state based on the present state and input.

The transition diagram in Figure 2 represents a finite state machine to recognize sequences that contain the word RHQ or QHM. Inputs, such as R and Q, label the edges; I - {R, Q} is the set of all amino acid symbols except R and Q. States, such as q0and q1, label the nodes. An arrow from node q0 to node q1 labeled with R indicates that if the machine is in state q0, an input R causes the machine to change to state q1. Because there is a loop from q0 to itself with the label I - {R, Q}, if in state q0, an input other than R or Q keeps the machine in state q0. The BLAST algorithm uses a DFA as a recognizer, or a machine that detects when an input sequence belongs to a particular set. We want to recognize any database sequence that contains a high scoring word. On the diagram, a double circle is around the final or accepting state(s), such as q5. If in scanning a sequence the DFA arrives at the final state q5, then the program accepts the sequence and notes the location of this high scoring word match, or seed, in the sequence. Then, beginning at s0, the program processes the rest of the sequence with the DFA to find other possible seeds. BLAST develops one DFA and processes each member of the database with this machine. The program notes all database sequences that the DFA accepts along with the locations of all seeds.

Figure 2. Finite state machine to recognize sequences that contain RHQ or QHM, where I is the set of one-letter symbols for the amino acids




Quick Review Question
Quick Review Question 5 Draw a transition diagram for a DFA to recognize any sequence that contains the 3-mer QQR.


Let us trace this DFA’s action in scanning NRSQHRHQLDLDMFPMST for RHQ or QHM. The machine starts in state q0, and the initial input of N keeps the machine in that state. The next input of R causes the machine to change to state q1, but S takes it back to q0. The inputs Q and then H cause the states to advance to q2 and then q4. The input R results in a cross over to state q1, and further inputs of H and Q carry the machine through state q3 to the accepting state of q5. Thus, RHQ is a seed in the database sequence NRSQHRHQLDLDMFPMST. BLAST notes the sequence and the location (6) of the seed (RHQ). The program then processes the rest of the sequence (LDLDMFPMST) starting at state q0 of the DFA. Because neither R nor Q appears in this subsequence, the machine remains in state q0. It is possible for two seeds to overlap, such as in RHQHM with one seed (RHQ) at location 1 and another (QHM) at location 3. However, because, the third major step of BLAST extends the seeds, we do not need to consider such an overlap and can start searching for additional seeds immediately after a located seed.

The following table summarizes the progress through the states to q5 for the given input:
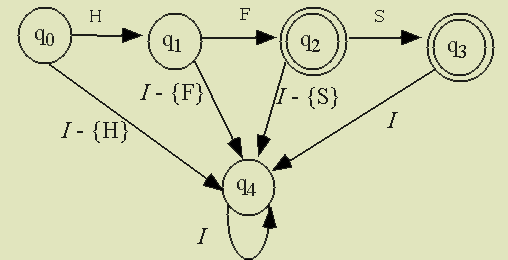
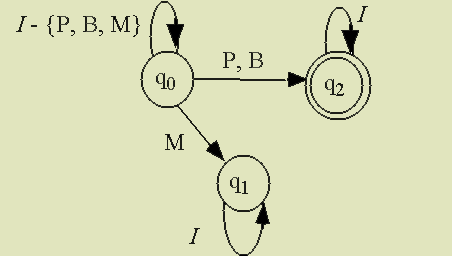
  input N R S Q H R H Q  
  state q0 q0 q1 q0 q2 q4 q1 q3 q5

The DFA performs rapidly. Hashing, which we consider in the exercises, is another excellent method of searching for seeds in database sequences. Primarily because the algorithm ignores gaps, the stage of scanning the protein database is quite fast, processing over a half-million amino acids per second.
Quick Review Question
Quick Review Question 6 Trace the action of Figure 2’s DFA in scanning QQHRVLRQHQHMMPY for RHQ or QHM.


The third step of the BLAST algorithm is to extend each of the seeds in both directions until the score reaches a maximum value. Using a heuristic, the program stops an extension if the score falls below a certain amount less than the highest score so far. For example, suppose the query sequence is in part ...SRMCDRHQMNCFPS..., and the program located high scoring word RHQ in the database sequence ...NRSQHRHQLDLDMF.... (xxx see p. 85 Should we include -5 or -6 score?) The following table shows how we extend from the seed RHQ to find a segment pair (DRHQMN and HRHQLD) with a maximum score (1 + 6 + 6 + 4 + 4 + 2 = 23):
In query: S D M C D R H Q M N C F P S
In database: N R S Q H R H Q L D L D M F
Score: 1 -1 -2 -5 1 6 6 4 4 2> -6 -6 -2 -3

DRHQMN and HRHQLD are a locally maximal segment pair, or a segment from the query sequence and a segment from a database sequence with a score that cannot become larger through shrinking or expanding the segments. We repeat this extension process for all seeds looking for all segment pairs with scores above some threshold. The algorithm is fast in part because it does not consider gaps and uses heuristics involving threshold values.
Quick Review Question
Quick Review Question 7 Find the locally maximal pair for the seed QHM in the database sequence QQHRVLRQHQHMMPY and the query sequence QACAHIRQNQHMIFD. Give the pair’s similarity score.

To summarize, the following are the steps of the BLAST algorithm:
Exercises

1. Using the Smith-Waterman algorithm with amino acid sequences s = AMFKVBYHR and t = MFKVYG, determine the best local alignment and its similarity score using the scoring of Example 1.

2.a. How many 4-mers are in a sequence of length 10?
   b. How many w-mers are in a sequence of length n?

3. Describe the set of strings recognized by the machine in Figure 3.

Figure 3. Machine for Exercises 3



4. Describe the set of strings recognized by the machine in Figure 4.

Figure 4 Machine for Exercises 4



5. Design a finite state machine to recognize any number of AT pairs. Thus, it recognizes the empty string, AT, ATAT, ATATAT, etc.

6. Design a finite state machine to recognize only an even number of C’s.

7. Repeat Exercise 6 for an odd number of C’s.

8. Design a finite state machine to recognize a 2-character sequence, where the first character is Q and the second is any amino acid or nothing.

9. Design a finite state machine to recognize a sequence ending with the amino acids BDS in that order.

10. Design a finite state machine to recognize a sequence starting with B.

11. Design a finite state machine to recognize a sequence that starts with C and has a G in the third position.

12. Another method of scanning a database utilizes hash tables. We can use the integers 0 through 22 to represent the amino acids, as follows:

 
A
B
C
D
E
F
G
H
I
K
L
M
N
P
Q
R
S
T
V
W
X
Y
Z
 
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

We can obtain a corresponding number for a 3-mer by using base 23 arithmetic. We add the product of the number for the first amino acid by 232 = 529, the product of the second number by 23, and the third number. For example, the number corresponding to the 3-mer ESK is 4 * 529 + 16 * 23 + 9 = 2493. Besides using a DFA, another fast way for scanning a database is to use a hash table to store the high scoring words from step 1 of the BLAST algorithm. Suppose there are 135 such 3-mers. We can store these words in a hash table of size prime size 199 and use the hash function h(n) = n % 199 with linear probing. Thus, ESK with value 2493 hashes to index 105, the remainder when we divide 199 into 2593. If a 3-mer is already in that location, we continue sequentially to the next locations until finding an available cell. To find seeds in a sequence, we compute the hash value of each sequence word and determine if the word is in the hash table or not. If it is in the table, the word is a seed.
a. Using this scheme, compute the number corresponding to PCV.
b. To what index does PCV hash?
13. For DNA, BLAST uses a word size of eleven bases. A typical BLAST similarity matrix uses a score of 5 for no evolution and a score of -4 for evolution. Thus, in the matrix, all diagonal elements are 5 and off-diagonal elements are -4.
a. Write this similarity matrix.
b. Give the 11-mers in the DNA sequence is ATTGTAATCCATCCCTAGGTTATAC.
c. Give the score of ATGGTACTCCG relative to the first 11-mer in the DNA sequence of Part b.
14. For DNA, a mutation between A and G or C and T, called a transition, is more likely to occur than a mutation between A and C, A and T, C and G, or G and T, called a transversion. A Transition/Transversion matrix, such as the one that follows, reflects such scoring:

 
A
C
G
T
A
-6
1
5
1
C
1
-6
1
5
G
5
1
-6
1
T
1
5
1
-6
 

Give the score of ATGGTACTCCG relative to the 11-mer ACTGTAATCCA.

Projects

1. Develop a program that uses the Smith-Waterman to find the best local alignment and its similarity score for pairs of sequences.

2. Develop a program to read a string of amino acid characters and to split the characters into a set of 2-mers. Score all 2-mers according to the 250 PAM. Display and store in a file all 2-mers that are above a score that the user enters.

3. Using the DFA of Figure 2, develop a program that searches a (xxx recommend one) relational database of sequences for seeds of RHQ or QHM. The program should store the sequences that contain RHQ or QHM and locations of these seeds in a relation.

4. For the relation in the previous project and for a query sequence that contains RHQ and QHM, return all locally maximal segment pairs along with their similarity scores.

5. Develop a program using the BLAST algorithm to return locally maximal segment pairs for a (xxx suggest one) DNA database and a query sequence. Use the scoring matrix of Exercise 13. Because there are only 4 bases, we can represent a nucleotide in 2 bits. For example, 00 might represent A, 01 C, 10 G, and 11 T. Thus, a byte of 8 bits can store four nucleotides instead of one character. Not only saving space, this compaction saves time because we can use bitwise operations to compare one byte at a time. Xxx

6. Read from a file or database a collection of amino acid triples and insert them into a hash table (see Exercise 12). Using hashing, search a collection for sequences for seeds. Store in a file or database each sequence that has a seed along with all its seeds and their locations.

Copyright © 2002, Dr. Angela B. Shiflet
All rights reserved